View libraries and data used in these notes
library(tidyverse)
library(DT)
library(GGally)
library(corrplot)
library(tidymodels)
library(glmnet) # ridge regression
trim32 = read_csv("https://sta221-fa25.github.io/data/trim32.csv")Ridge regression
Data
dim(trim32)[1] 120 501The data come from a gene expression study by Scheetz et al. (2006, Genome Biology, 7:R62), which examined gene regulation in rat eye tissue.
In this data set, we have measurements from 120 rats, each with expression levels recorded for 500 genes. These 500 genes serve as our predictor variables. The outcome of interest is the expression level of a specific gene called TRIM32, which plays a role in retinal development. Moreover, TRIM32 is known to be linked with a genetic disorder called Bardet-Biedl Syndrome (BBS): the mutation (P130S) in Trim32 gives rise to BBS. Thus, each observation corresponds to one rat, with TRIM32 expression as a continuous response variable and 500 other gene expression levels as predictors.
Naive fit: which genes matter?
fit = lm(y ~ 0 + ., data = trim32)
summary(fit)
Call:
lm(formula = y ~ 0 + ., data = trim32)
Residuals:
ALL 120 residuals are 0: no residual degrees of freedom!
Coefficients: (380 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
`1367539_at` 2.46865 NaN NaN NaN
`1367566_at` 1.99593 NaN NaN NaN
`1368099_at` -6.18590 NaN NaN NaN
`1368114_at` -1.56565 NaN NaN NaN
`1368136_at` -0.10125 NaN NaN NaN
`1368175_at` -0.96281 NaN NaN NaN
`1368177_at` -1.62396 NaN NaN NaN
`1368216_at` 3.14747 NaN NaN NaN
`1368225_at` -0.50621 NaN NaN NaN
`1368229_at` 3.34274 NaN NaN NaN
`1368476_at` 0.69985 NaN NaN NaN
`1368898_at` -0.42802 NaN NaN NaN
`1369018_at` -0.63656 NaN NaN NaN
`1369210_at` 1.12077 NaN NaN NaN
`1369237_at` -0.74250 NaN NaN NaN
`1370205_at` 0.08702 NaN NaN NaN
`1370354_at` 1.67294 NaN NaN NaN
`1370429_at` -0.03392 NaN NaN NaN
`1370437_at` -1.70450 NaN NaN NaN
`1370439_a_at` 3.98168 NaN NaN NaN
`1370551_a_at` -0.01096 NaN NaN NaN
`1370555_at` 4.07083 NaN NaN NaN
`1370827_at` 2.42265 NaN NaN NaN
`1371072_at` 2.02812 NaN NaN NaN
`1371133_a_at` 1.59933 NaN NaN NaN
`1371610_at` 1.37769 NaN NaN NaN
`1371614_at` 7.60068 NaN NaN NaN
`1371661_at` -1.53753 NaN NaN NaN
`1371828_at` 0.99506 NaN NaN NaN
`1371953_at` -2.81015 NaN NaN NaN
`1371963_at` 2.68767 NaN NaN NaN
`1372022_at` 0.68078 NaN NaN NaN
`1372046_at` -2.10084 NaN NaN NaN
`1372072_at` 0.85047 NaN NaN NaN
`1372078_at` -3.77567 NaN NaN NaN
`1372081_at` 4.40179 NaN NaN NaN
`1372104_at` -2.33684 NaN NaN NaN
`1372121_at` -3.38501 NaN NaN NaN
`1372143_at` -0.23154 NaN NaN NaN
`1372189_at` 2.46281 NaN NaN NaN
`1372192_at` -4.08633 NaN NaN NaN
`1372202_at` 1.25190 NaN NaN NaN
`1372248_at` 2.07958 NaN NaN NaN
`1372266_at` 1.69119 NaN NaN NaN
`1372329_at` 0.53905 NaN NaN NaN
`1372445_at` -4.53436 NaN NaN NaN
`1372449_at` -4.86333 NaN NaN NaN
`1372453_at` 3.30659 NaN NaN NaN
`1372463_at` -4.53623 NaN NaN NaN
`1372497_at` -8.59019 NaN NaN NaN
`1372538_at` 1.57537 NaN NaN NaN
`1372544_at` -1.08486 NaN NaN NaN
`1372563_at` 0.16883 NaN NaN NaN
`1372582_at` 6.01114 NaN NaN NaN
`1372594_at` -3.02689 NaN NaN NaN
`1372633_at` 0.56998 NaN NaN NaN
`1372674_at` -2.07716 NaN NaN NaN
`1372675_at` 3.87690 NaN NaN NaN
`1372710_at` 1.13940 NaN NaN NaN
`1372713_at` 3.95023 NaN NaN NaN
`1372715_at` -4.67805 NaN NaN NaN
`1372733_at` 1.11764 NaN NaN NaN
`1372768_at` 2.46896 NaN NaN NaN
`1372816_at` 2.07744 NaN NaN NaN
`1372817_at` 5.15885 NaN NaN NaN
`1372830_at` 2.48010 NaN NaN NaN
`1372867_at` -1.38762 NaN NaN NaN
`1372921_at` 5.76248 NaN NaN NaN
`1372928_at` -0.14972 NaN NaN NaN
`1372953_at` -4.46764 NaN NaN NaN
`1373039_at` -4.84993 NaN NaN NaN
`1373083_at` -0.33033 NaN NaN NaN
`1373136_at` -4.77394 NaN NaN NaN
`1373163_at` 0.14398 NaN NaN NaN
`1373165_at` -1.33642 NaN NaN NaN
`1373194_at` -2.98023 NaN NaN NaN
`1373200_at` 2.76554 NaN NaN NaN
`1373272_at` -0.09018 NaN NaN NaN
`1373326_at` -0.71469 NaN NaN NaN
`1373327_at` 2.05675 NaN NaN NaN
`1373333_at` -1.84414 NaN NaN NaN
`1373336_at` 3.76057 NaN NaN NaN
`1373381_at` -2.16455 NaN NaN NaN
`1373398_at` 0.90460 NaN NaN NaN
`1373431_at` -2.24258 NaN NaN NaN
`1373441_at` -0.10277 NaN NaN NaN
`1373450_at` 2.91785 NaN NaN NaN
`1373472_at` -0.57352 NaN NaN NaN
`1373519_at` -1.61598 NaN NaN NaN
`1373534_at` -4.05563 NaN NaN NaN
`1373545_at` -2.35288 NaN NaN NaN
`1373569_at` -1.33591 NaN NaN NaN
`1373621_at` 3.04496 NaN NaN NaN
`1373643_at` -0.20441 NaN NaN NaN
`1373677_at` 3.91286 NaN NaN NaN
`1373683_at` 0.64733 NaN NaN NaN
`1373707_at` 1.43368 NaN NaN NaN
`1373771_at` -0.33101 NaN NaN NaN
`1373784_at` -1.24218 NaN NaN NaN
`1373813_at` 0.61754 NaN NaN NaN
`1373835_at` -1.31505 NaN NaN NaN
`1373843_at` -1.45044 NaN NaN NaN
`1373859_at` -0.85743 NaN NaN NaN
`1373887_at` 2.74729 NaN NaN NaN
`1373912_at` 0.66126 NaN NaN NaN
`1373941_at` 1.52398 NaN NaN NaN
`1373944_at` 0.40778 NaN NaN NaN
`1374010_at` 2.04752 NaN NaN NaN
`1374027_at` -0.32516 NaN NaN NaN
`1374074_at` -2.22232 NaN NaN NaN
`1374094_at` 0.33973 NaN NaN NaN
`1374106_at` -0.68325 NaN NaN NaN
`1374150_at` 0.90613 NaN NaN NaN
`1374151_at` 1.33677 NaN NaN NaN
`1374187_at` 2.00123 NaN NaN NaN
`1374233_at` -4.76009 NaN NaN NaN
`1374401_at` 0.02641 NaN NaN NaN
`1374423_at` -3.22747 NaN NaN NaN
`1374519_at` -2.31308 NaN NaN NaN
`1374542_at` 0.76899 NaN NaN NaN
`1374548_at` NA NA NA NA
`1374574_at` NA NA NA NA
`1374581_at` NA NA NA NA
`1374628_at` NA NA NA NA
`1374645_at` NA NA NA NA
`1374647_at` NA NA NA NA
`1374669_at` NA NA NA NA
`1374766_at` NA NA NA NA
`1374792_at` NA NA NA NA
`1374809_at` NA NA NA NA
`1374890_at` NA NA NA NA
`1375035_at` NA NA NA NA
`1375036_at` NA NA NA NA
`1375056_at` NA NA NA NA
`1375129_at` NA NA NA NA
`1375389_at` NA NA NA NA
`1375431_at` NA NA NA NA
`1375510_x_at` NA NA NA NA
`1375638_at` NA NA NA NA
`1375743_at` NA NA NA NA
`1375832_at` NA NA NA NA
`1375833_at` NA NA NA NA
`1375841_at` NA NA NA NA
`1375894_at` NA NA NA NA
`1375965_at` NA NA NA NA
`1376004_at` NA NA NA NA
`1376086_at` NA NA NA NA
`1376121_at` NA NA NA NA
`1376125_at` NA NA NA NA
`1376159_at` NA NA NA NA
`1376261_at` NA NA NA NA
`1376306_at` NA NA NA NA
`1376336_at` NA NA NA NA
`1376374_at` NA NA NA NA
`1376376_at` NA NA NA NA
`1376551_at` NA NA NA NA
`1376584_at` NA NA NA NA
`1376587_at` NA NA NA NA
`1376637_at` NA NA NA NA
`1376641_at` NA NA NA NA
`1376683_at` NA NA NA NA
`1376686_at` NA NA NA NA
`1376687_at` NA NA NA NA
`1376714_at` NA NA NA NA
`1376747_at` NA NA NA NA
`1376773_at` NA NA NA NA
`1376832_at` NA NA NA NA
`1376842_at` NA NA NA NA
`1376945_at` NA NA NA NA
`1376984_at` NA NA NA NA
`1377005_at` NA NA NA NA
`1377043_at` NA NA NA NA
`1377127_at` NA NA NA NA
`1377128_at` NA NA NA NA
`1377141_at` NA NA NA NA
`1377157_at` NA NA NA NA
`1377162_at` NA NA NA NA
`1377194_a_at` NA NA NA NA
`1377236_at` NA NA NA NA
`1377254_a_at` NA NA NA NA
`1377273_at` NA NA NA NA
`1377281_at` NA NA NA NA
`1377327_at` NA NA NA NA
`1377469_at` NA NA NA NA
`1377836_at` NA NA NA NA
`1379451_at` NA NA NA NA
`1379580_at` NA NA NA NA
`1380466_at` NA NA NA NA
`1382223_at` NA NA NA NA
`1382345_at` NA NA NA NA
`1383192_at` NA NA NA NA
`1383383_at` NA NA NA NA
`1383561_at` NA NA NA NA
`1383649_a_at` NA NA NA NA
`1384065_at` NA NA NA NA
`1384584_at` NA NA NA NA
`1385697_at` NA NA NA NA
`1385826_at` NA NA NA NA
`1386358_at` NA NA NA NA
`1387142_at` NA NA NA NA
`1387262_at` NA NA NA NA
`1387501_at` NA NA NA NA
`1387527_at` NA NA NA NA
`1387781_at` NA NA NA NA
`1387977_at` NA NA NA NA
`1388087_at` NA NA NA NA
`1388135_at` NA NA NA NA
`1388383_at` NA NA NA NA
`1388491_at` NA NA NA NA
`1388656_at` NA NA NA NA
`1388743_at` NA NA NA NA
`1388796_at` NA NA NA NA
`1388799_at` NA NA NA NA
`1388830_at` NA NA NA NA
`1388929_at` NA NA NA NA
`1388996_at` NA NA NA NA
`1388999_at` NA NA NA NA
`1389049_at` NA NA NA NA
`1389057_at` NA NA NA NA
`1389082_at` NA NA NA NA
`1389133_at` NA NA NA NA
`1389153_at` NA NA NA NA
`1389205_at` NA NA NA NA
`1389225_at` NA NA NA NA
`1389226_at` NA NA NA NA
`1389229_at` NA NA NA NA
`1389241_at` NA NA NA NA
`1389254_at` NA NA NA NA
`1389275_at` NA NA NA NA
`1389329_at` NA NA NA NA
`1389357_at` NA NA NA NA
`1389388_at` NA NA NA NA
`1389428_at` NA NA NA NA
`1389457_at` NA NA NA NA
`1389460_at` NA NA NA NA
`1389539_at` NA NA NA NA
`1389549_at` NA NA NA NA
`1389584_at` NA NA NA NA
`1389607_at` NA NA NA NA
`1389730_at` NA NA NA NA
`1389763_at` NA NA NA NA
`1389781_at` NA NA NA NA
`1389910_at` NA NA NA NA
`1389915_at` NA NA NA NA
`1389968_at` NA NA NA NA
`1389978_at` NA NA NA NA
`1389981_at` NA NA NA NA
`1390142_at` NA NA NA NA
`1390272_at` NA NA NA NA
`1390301_at` NA NA NA NA
`1390323_at` NA NA NA NA
`1390394_at` NA NA NA NA
`1390427_at` NA NA NA NA
`1390439_at` NA NA NA NA
`1390456_at` NA NA NA NA
`1390539_at` NA NA NA NA
`1390574_at` NA NA NA NA
`1390599_at` NA NA NA NA
`1390709_at` NA NA NA NA
`1391096_at` NA NA NA NA
`1391408_a_at` NA NA NA NA
`1391412_at` NA NA NA NA
`1391454_at` NA NA NA NA
`1391484_at` NA NA NA NA
`1392749_at` NA NA NA NA
`1392958_at` NA NA NA NA
`1393251_at` NA NA NA NA
`1398308_at` NA NA NA NA
`1398337_at` NA NA NA NA
`1398340_at` NA NA NA NA
`1398370_at` NA NA NA NA
`1398384_at` NA NA NA NA
`1398395_at` NA NA NA NA
`1398396_at` NA NA NA NA
`1398405_at` NA NA NA NA
`1398409_at` NA NA NA NA
`1398447_at` NA NA NA NA
`1398448_at` NA NA NA NA
`1398988_at` NA NA NA NA
`1399061_at` NA NA NA NA
`1399114_at` NA NA NA NA
`1399134_at` NA NA NA NA
`1399154_at` NA NA NA NA
`1377569_at` NA NA NA NA
`1377596_a_at` NA NA NA NA
`1377637_at` NA NA NA NA
`1377644_at` NA NA NA NA
`1377681_at` NA NA NA NA
`1377701_at` NA NA NA NA
`1377745_at` NA NA NA NA
`1377755_at` NA NA NA NA
`1377757_at` NA NA NA NA
`1377786_at` NA NA NA NA
`1377791_at` NA NA NA NA
`1377880_at` NA NA NA NA
`1377883_at` NA NA NA NA
`1377919_at` NA NA NA NA
`1378022_at` NA NA NA NA
`1378036_at` NA NA NA NA
`1378125_at` NA NA NA NA
`1378185_at` NA NA NA NA
`1378316_at` NA NA NA NA
`1378578_at` NA NA NA NA
`1378590_at` NA NA NA NA
`1378620_at` NA NA NA NA
`1378680_at` NA NA NA NA
`1378741_at` NA NA NA NA
`1378819_at` NA NA NA NA
`1378928_at` NA NA NA NA
`1379029_at` NA NA NA NA
`1379094_at` NA NA NA NA
`1379121_at` NA NA NA NA
`1379169_at` NA NA NA NA
`1379187_at` NA NA NA NA
`1379279_at` NA NA NA NA
`1379283_at` NA NA NA NA
`1379290_at` NA NA NA NA
`1379476_at` NA NA NA NA
`1379495_at` NA NA NA NA
`1379600_at` NA NA NA NA
`1379625_at` NA NA NA NA
`1379693_at` NA NA NA NA
`1379699_at` NA NA NA NA
`1379728_at` NA NA NA NA
`1379971_at` NA NA NA NA
`1379982_at` NA NA NA NA
`1380058_at` NA NA NA NA
`1380174_at` NA NA NA NA
`1380185_at` NA NA NA NA
`1380214_at` NA NA NA NA
`1380233_x_at` NA NA NA NA
`1380402_at` NA NA NA NA
`1380463_at` NA NA NA NA
`1380477_at` NA NA NA NA
`1380553_at` NA NA NA NA
`1380794_at` NA NA NA NA
`1380811_at` NA NA NA NA
`1380815_at` NA NA NA NA
`1380852_at` NA NA NA NA
`1380890_at` NA NA NA NA
`1380932_at` NA NA NA NA
`1381077_at` NA NA NA NA
`1381481_at` NA NA NA NA
`1381755_x_at` NA NA NA NA
`1381849_at` NA NA NA NA
`1381902_at` NA NA NA NA
`1381914_at` NA NA NA NA
`1381926_at` NA NA NA NA
`1381930_at` NA NA NA NA
`1381963_at` NA NA NA NA
`1381976_at` NA NA NA NA
`1381998_at` NA NA NA NA
`1382045_at` NA NA NA NA
`1382065_at` NA NA NA NA
`1382114_at` NA NA NA NA
`1382132_at` NA NA NA NA
`1382139_at` NA NA NA NA
`1382154_at` NA NA NA NA
`1382271_at` NA NA NA NA
`1382290_at` NA NA NA NA
`1382379_at` NA NA NA NA
`1382517_at` NA NA NA NA
`1382579_at` NA NA NA NA
`1382651_at` NA NA NA NA
`1382779_at` NA NA NA NA
`1383081_at` NA NA NA NA
`1383084_at` NA NA NA NA
`1383110_at` NA NA NA NA
`1383167_at` NA NA NA NA
`1383172_at` NA NA NA NA
`1383226_at` NA NA NA NA
`1383236_at` NA NA NA NA
`1383249_at` NA NA NA NA
`1383254_at` NA NA NA NA
`1383257_at` NA NA NA NA
`1383299_at` NA NA NA NA
`1383374_at` NA NA NA NA
`1383431_at` NA NA NA NA
`1383433_at` NA NA NA NA
`1383504_at` NA NA NA NA
`1383533_at` NA NA NA NA
`1383607_at` NA NA NA NA
`1383611_at` NA NA NA NA
`1383673_at` NA NA NA NA
`1383720_at` NA NA NA NA
`1383731_at` NA NA NA NA
`1383783_at` NA NA NA NA
`1383998_at` NA NA NA NA
`1384007_at` NA NA NA NA
`1384035_at` NA NA NA NA
`1384150_at` NA NA NA NA
`1384205_at` NA NA NA NA
`1384222_at` NA NA NA NA
`1384247_at` NA NA NA NA
`1384296_at` NA NA NA NA
`1384320_at` NA NA NA NA
`1384352_at` NA NA NA NA
`1384368_at` NA NA NA NA
`1384382_at` NA NA NA NA
`1384387_at` NA NA NA NA
`1384542_at` NA NA NA NA
`1384565_at` NA NA NA NA
`1384860_at` NA NA NA NA
`1384940_at` NA NA NA NA
`1385030_at` NA NA NA NA
`1385106_at` NA NA NA NA
`1385168_at` NA NA NA NA
`1385261_s_at` NA NA NA NA
`1385501_at` NA NA NA NA
`1385559_at` NA NA NA NA
`1385597_at` NA NA NA NA
`1385776_at` NA NA NA NA
`1385798_at` NA NA NA NA
`1385883_at` NA NA NA NA
`1386248_at` NA NA NA NA
`1386683_at` NA NA NA NA
`1390779_at` NA NA NA NA
`1390799_at` NA NA NA NA
`1390814_at` NA NA NA NA
`1390836_at` NA NA NA NA
`1390856_at` NA NA NA NA
`1390864_at` NA NA NA NA
`1390868_at` NA NA NA NA
`1390874_at` NA NA NA NA
`1390875_a_at` NA NA NA NA
`1390945_at` NA NA NA NA
`1391005_at` NA NA NA NA
`1391013_at` NA NA NA NA
`1391085_at` NA NA NA NA
`1391092_at` NA NA NA NA
`1391101_at` NA NA NA NA
`1391155_at` NA NA NA NA
`1391183_at` NA NA NA NA
`1391212_at` NA NA NA NA
`1391271_at` NA NA NA NA
`1391308_at` NA NA NA NA
`1391415_at` NA NA NA NA
`1391443_at` NA NA NA NA
`1391464_at` NA NA NA NA
`1391475_at` NA NA NA NA
`1391564_at` NA NA NA NA
`1391727_at` NA NA NA NA
`1391928_at` NA NA NA NA
`1392199_at` NA NA NA NA
`1392313_at` NA NA NA NA
`1392470_at` NA NA NA NA
`1392573_at` NA NA NA NA
`1392599_at` NA NA NA NA
`1392601_at` NA NA NA NA
`1392610_at` NA NA NA NA
`1392698_a_at` NA NA NA NA
`1392772_at` NA NA NA NA
`1392911_at` NA NA NA NA
`1392918_at` NA NA NA NA
`1392982_at` NA NA NA NA
`1392997_at` NA NA NA NA
`1393019_at` NA NA NA NA
`1393027_at` NA NA NA NA
`1393051_at` NA NA NA NA
`1393149_at` NA NA NA NA
`1393218_at` NA NA NA NA
`1393258_at` NA NA NA NA
`1393366_at` NA NA NA NA
`1393510_at` NA NA NA NA
`1393666_at` NA NA NA NA
`1393736_at` NA NA NA NA
`1393794_at` NA NA NA NA
`1393803_at` NA NA NA NA
`1393817_at` NA NA NA NA
`1393977_at` NA NA NA NA
`1394095_at` NA NA NA NA
`1394192_at` NA NA NA NA
`1394455_at` NA NA NA NA
`1394505_at` NA NA NA NA
`1394884_s_at` NA NA NA NA
`1394897_at` NA NA NA NA
`1395285_at` NA NA NA NA
`1395455_at` NA NA NA NA
`1395469_at` NA NA NA NA
`1395479_at` NA NA NA NA
`1395504_at` NA NA NA NA
`1395647_at` NA NA NA NA
`1395779_at` NA NA NA NA
`1395791_at` NA NA NA NA
`1396123_at` NA NA NA NA
`1396476_at` NA NA NA NA
`1396678_at` NA NA NA NA
`1396853_at` NA NA NA NA
`1396920_at` NA NA NA NA
`1397227_at` NA NA NA NA
`1397325_at` NA NA NA NA
`1397363_at` NA NA NA NA
`1397438_at` NA NA NA NA
`1397554_at` NA NA NA NA
`1397932_at` NA NA NA NA
`1397946_at` NA NA NA NA
`1397995_at` NA NA NA NA
`1398601_at` NA NA NA NA
`1398639_at` NA NA NA NA
`1398663_at` NA NA NA NA
Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: NaN
F-statistic: NaN on 120 and 0 DF, p-value: NAsmall_subset = trim32 %>%
select(y,`1397932_at`, `1394095_at`,`1393803_at`) %>%
.[1:2,]
small_subset# A tibble: 2 × 4
y `1397932_at` `1394095_at` `1393803_at`
<dbl> <dbl> <dbl> <dbl>
1 8.38 4.80 5.84 6.49
2 8.27 4.72 6.19 6.68small_subset %>%
lm(y ~ 0 + `1397932_at` + `1394095_at` + `1393803_at`, data = .) %>%
summary()
Call:
lm(formula = y ~ 0 + `1397932_at` + `1394095_at` + `1393803_at`,
data = .)
Residuals:
ALL 2 residuals are 0: no residual degrees of freedom!
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
`1397932_at` 1.70996 NaN NaN NaN
`1394095_at` 0.03045 NaN NaN NaN
`1393803_at` NA NA NA NA
Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: NaN
F-statistic: NaN on 2 and 0 DF, p-value: NA\[ \begin{aligned} y_1 &= \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3\\ y_2 &= \beta_1 x_1 + \beta2 x_2 + \beta_3 x_3 \end{aligned} \] - \(p > n\) \(\implies\) linearly dependent columns \(\implies\) infinitely many solutions!
- Put another way, the rank of \(X^TX\) is a \(p \times p\) matrix of rank \(n < p\), which means we cannot invert it and find a unique least-squares solution.
Question: What would be nice to do, to fix this, intuitively?
Question: What would be nice to do, to fix this, mathematically?
Fix the model
Re-formulating the optimization problem
Intuitively, we have too many predictors, and we want fewer. We could enforce this by shrinking some of the elements of \(\beta\) towards zero. Practically, this would reduce the size of the \(\beta\) vector. We can do this by modifying our objective function:
\[ \hat{\beta}_{ridge} = \underset{\beta}{\operatorname{argmin}} \underbrace{(\boldsymbol{y}- \boldsymbol{X}\beta)^T (\boldsymbol{y}- \boldsymbol{X}\beta)}_{\text{RSS}} + \lambda \underbrace{\beta^T\beta}_{\text{penalty}} \] where \(\lambda > 0\) is a parameter that we, as the statistician, must specify. What does this parameter do? What happens at the boundaries \(\lambda \rightarrow 0\) and \(\lambda \rightarrow \infty\)?
The picture: what’s happening?
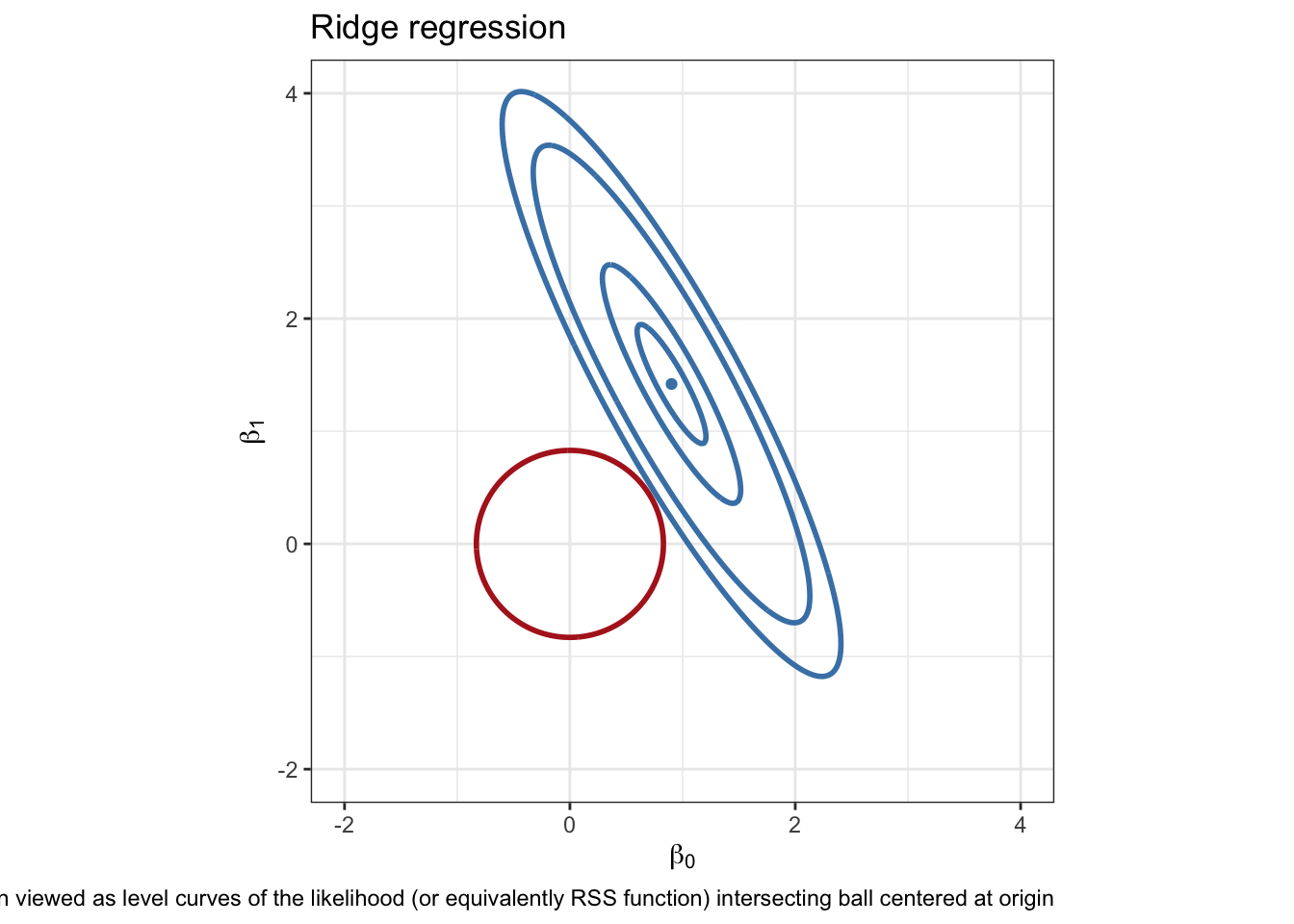
For any given \(\lambda\), the set of solutions is constrained to the ball \(||\beta||_2^2 \leq c^2\), for some constant \(c\). Note: \(||\beta||_2 = \sqrt{\sum_{i=1}^p \beta_i^2}\).
- What happens if \(c^2 \geq ||\hat{\beta}_{OLS}||_2^2\)?
- What is the “level curve” of a function?
- Why do the level curves look like an ellipse?
- Consider: what if predictors are on very different scales, i.e. \(x_1 >> x_2\)?
What is the ridge regression solution?
Derive the ridge-regression solution.
\[ \hat{\beta}_{ridge} = (\boldsymbol{X}^T\boldsymbol{X}) + \lambda \boldsymbol{I})^{-1} \boldsymbol{X}^T \boldsymbol{y} \]
- Algebraically, we have “fixed” the troublesome singular matrix \((\boldsymbol{X}^T \boldsymbol{X})\) by adding a positive constant \(\lambda\) to its diagonal.
- What is \(E[\hat{\beta}_{ridge}]\)? Is it a biased or unbiased estimator of \(\beta\)?
Computing manually
# get X matrix (no intercept)
X = model.matrix(y ~ 0 + ., data = trim32)
Xs = scale(X)
XTX = t(Xs) %*% Xs
y = trim32$y %>%
as.matrix(ncol = 1)
p = nrow(XTX)
lambda = 1
betahat_ridge = solve(XTX + diag(lambda, nrow = p)) %*% t(Xs) %*% y betahat_ridge %>%
as.data.frame() %>%
arrange(desc(abs(V1))) %>%
head(n = 5) V1
`1389910_at` 0.01344827
`1374423_at` -0.01276357
`1388491_at` 0.01199265
`1372453_at` 0.01178389
`1389241_at` -0.01169062Using a package
lm.ridge() within the MASS package
Warning
MASS has a function select() that will cause issues with dplyr’s select. For this reason it is preferable to not load both libraries simultaneously.
# pass standardized data in:
ridge_fit = MASS::lm.ridge(y ~ 0 + ., data = data.frame(y, Xs),
lambda = 1)
beta_scaled_lmridge = ridge_fit$coef # scaled space coefficients
beta_unscaled_lmridge = coef(ridge_fit) # original scale coefficients
# (different than computed above if y and X are not standardized inputs)
beta_unscaled_lmridge[1:4]X.1367539_at. X.1367566_at. X.1368099_at. X.1368114_at.
0.0015121170 -0.0027627847 -0.0026806299 0.0005469267 beta_scaled_lmridge[1:4]X.1367539_at. X.1367566_at. X.1368099_at. X.1368114_at.
0.0015058034 -0.0027512491 -0.0026694372 0.0005446431 betahat_ridge[1:4,]`1367539_at` `1367566_at` `1368099_at` `1368114_at`
0.001511725 -0.002762699 -0.002679906 0.000546758
Warning
coef(ridge_fit) and ridge_fit$coef return unscaled and scaled coefficients respectively.
Using a different package
Alternatively, could use glmnet() within the glmnet package. The function glmnet is not just for ridge regression but can perform other forms of penalized regression. Setting alpha = 0 maps the objective to a ridge regression problem.
Warning
The argument \(\lambda\) in glmnet() is different. Specifically, the objective function used in glmnet is
\[ \arg \min_{\beta} ~\frac{1}{n} RSS + \lambda \beta^T\beta \]
So, \(\lambda \times n\) where \(n\) is the number of observations, nrow(X), will match the same objective function.
X = scale(model.matrix(y ~ 0 + ., data = trim32))
XTX = t(X) %*% X
y = trim32$y %>%
as.matrix(ncol = 1) %>%
scale()
p = nrow(XTX)
lambda = 100
betahat_ridge = solve(XTX + diag(lambda * nrow(X), nrow = p)) %*% t(X) %*% y
betahat_ridge[1:4,]`1367539_at` `1367566_at` `1368099_at` `1368114_at`
0.001605039 -0.002256027 0.001665459 0.001521466 fit = glmnet::glmnet(X, y, alpha = 0, # alpha = 0 defines ridge reg.
lambda = lambda,
intercept = FALSE)
fit$beta[1:4,]`1367539_at` `1367566_at` `1368099_at` `1368114_at`
0.001637818 -0.002290652 0.001700664 0.001555549 Ridge plots (how to choose \(\lambda\)?)
## 1. Fit for a sequence of lambdas
lambdas = seq(0, 5, length = 100)
ridge_fit = MASS::lm.ridge(y ~ 0 + ., data = trim32, lambda = lambdas)
# 2. Plot ridge trace
plot(ridge_fit, main = "Ridge Trace Plot")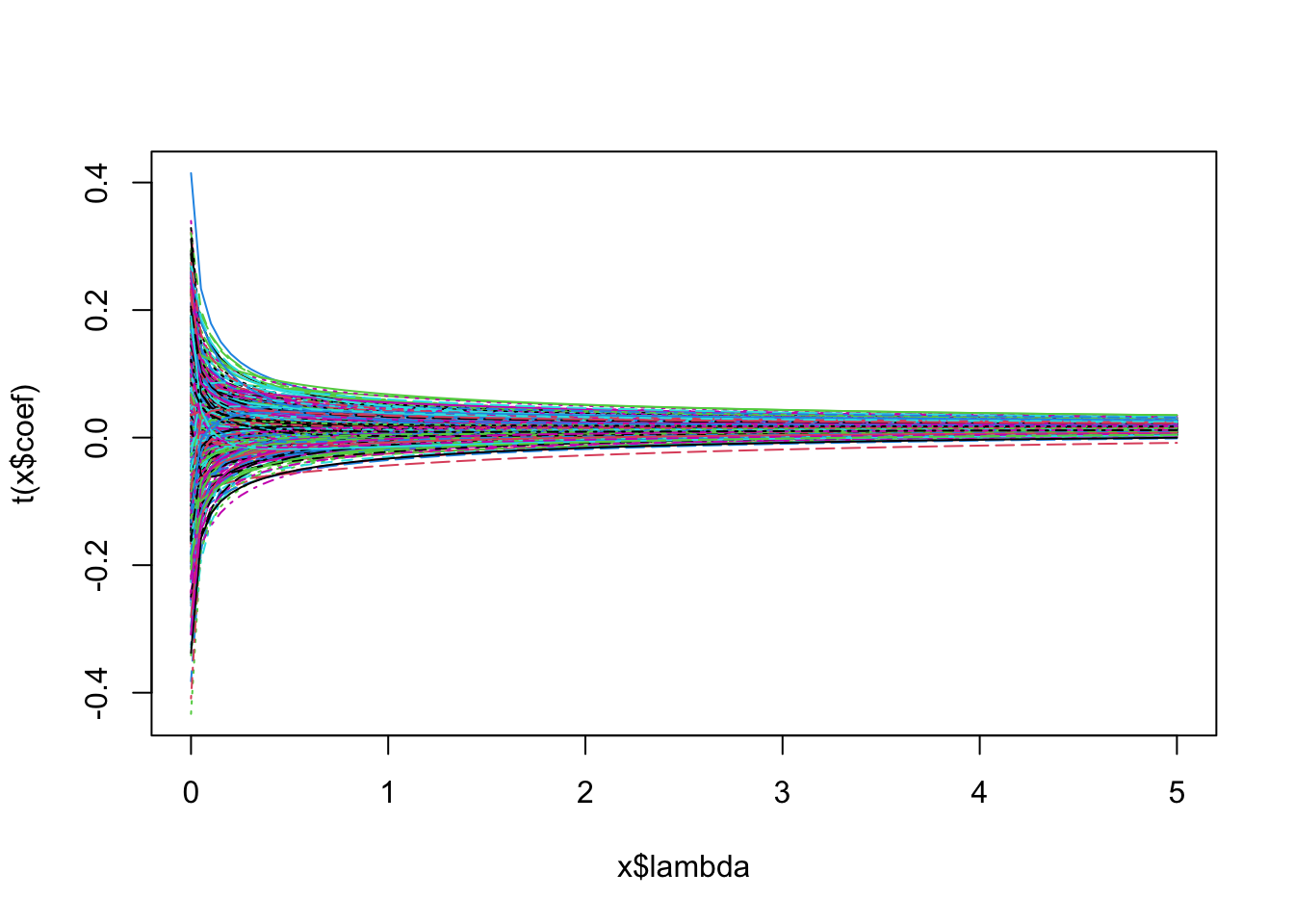
MASS::select(ridge_fit) # find lambda that minimizes GCVmodified HKB estimator is -1.460229e-27
modified L-W estimator is -2.215401e-28
smallest value of GCV at 0.2525253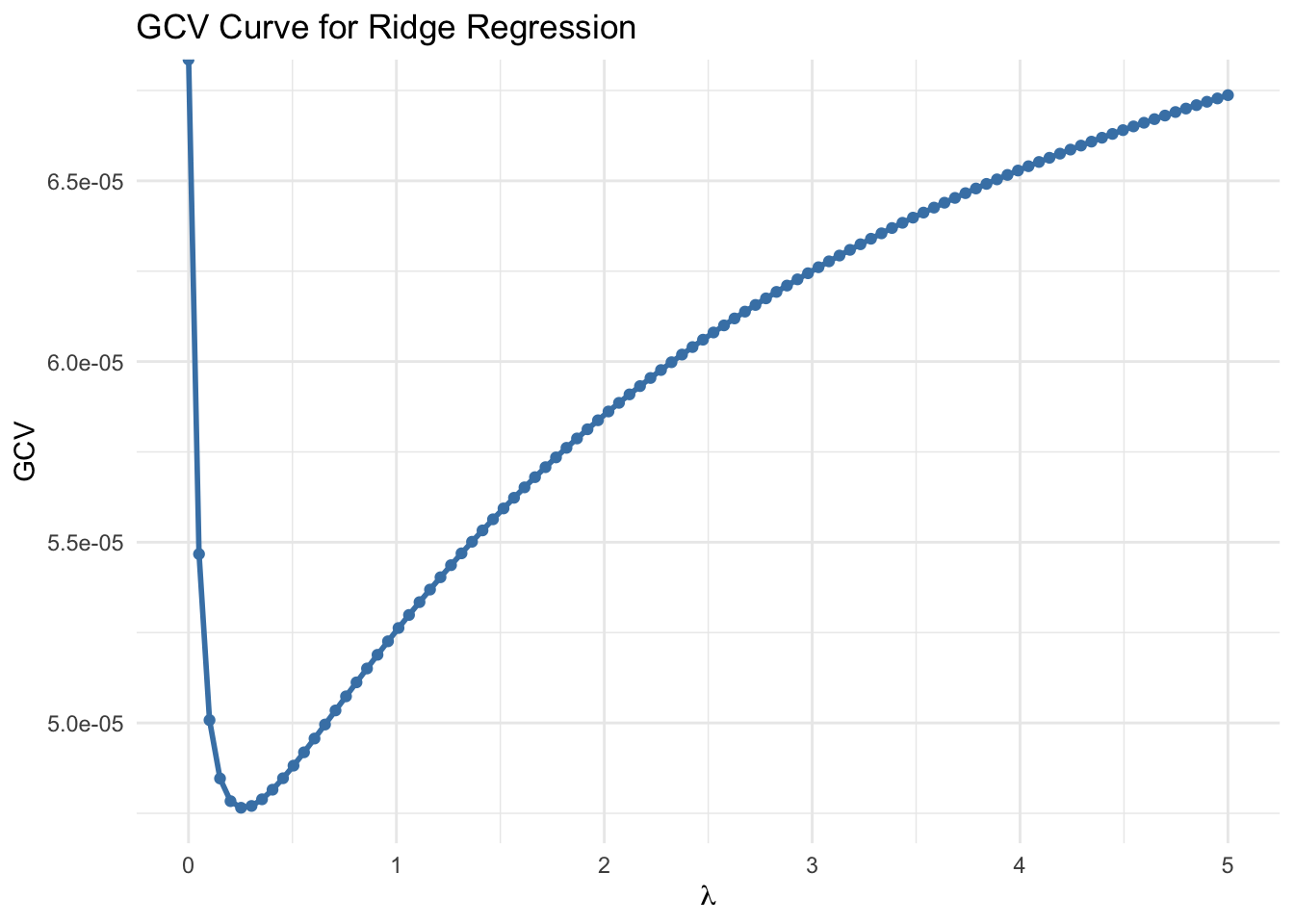 
- Generalized cross validation (GCV) is an approximation to leave 1 out cross-validation, but does not require re-computing the model \(n\) times for each \(\lambda\).
What is GCV and why does it work?
In ridge regression the fitted values can be written as
\[ \hat{y} = H_\lambda y, \]
where \(H_\lambda\) is the hat matrix depending on \(\lambda\).
In order to compute the average leave-one-out cross-validation error for a given \(\lambda\) requires computing the residual for each observation \(i\) when the model is refit without that point:
\[ \text{CV}(\lambda) = \frac{1}{n}\sum_{i=1}^n \left( \frac{y_i - \hat{y}_i}{1 - h_{ii}(\lambda)} \right)^2, \]
where \(h_{ii}\) is the \(i\)th diagonal element of \(H_\lambda\).
Generalized cross-validation (GCV) replaces the individual \(h_{ii}\) values with their average \(\mathrm{tr}(H_\lambda)/n\):
\[ \text{GCV}(\lambda) = \frac{\tfrac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2} {\left(1 - \tfrac{\mathrm{tr}(H_\lambda)}{n}\right)^2}. \]
Vocabulary and further reading
Broadly ridge regression is a form of “penalized regression” and is often called “regularization”. The other two most common forms of regularization are “lasso regularization” and best subset selection. These correspond to an L-1 and L-0 penalty respectively.
Since the expected value of the ridge regression estimator is not equal to \(\beta\), it is sometimes referred to as a method of biased estimation. Often, we trade a small amount of bias for reduced variability in the estimator. This trade-off is called the bias-variance trade-off.
The seminal ridge regression paper: Hoerl and Kennard 1970 and a better format.