Rows: 456
Columns: 13
$ `Player Name` <chr> "Stephen Curry", "John Wall", "Russell Westbrook", "LeBr…
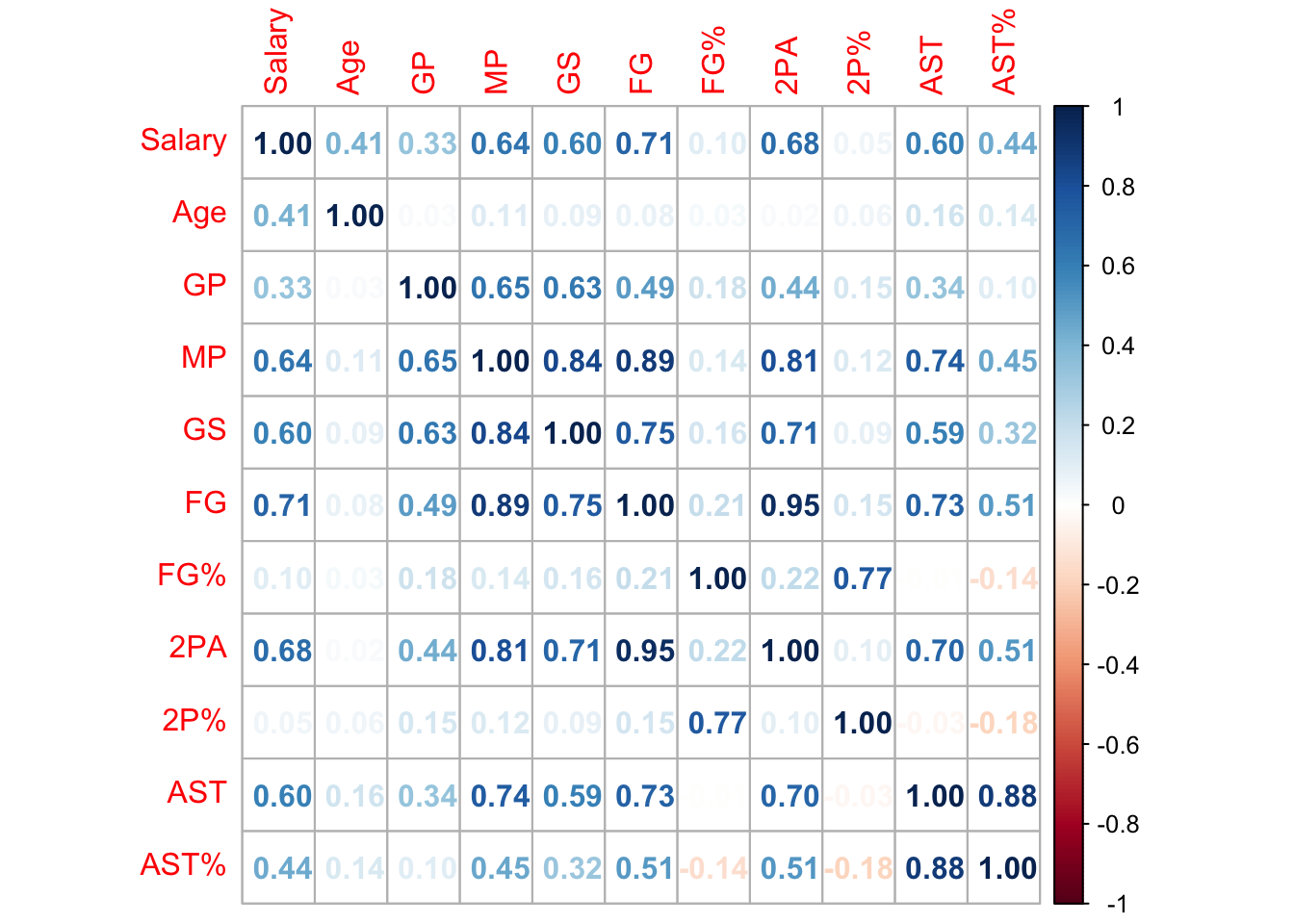
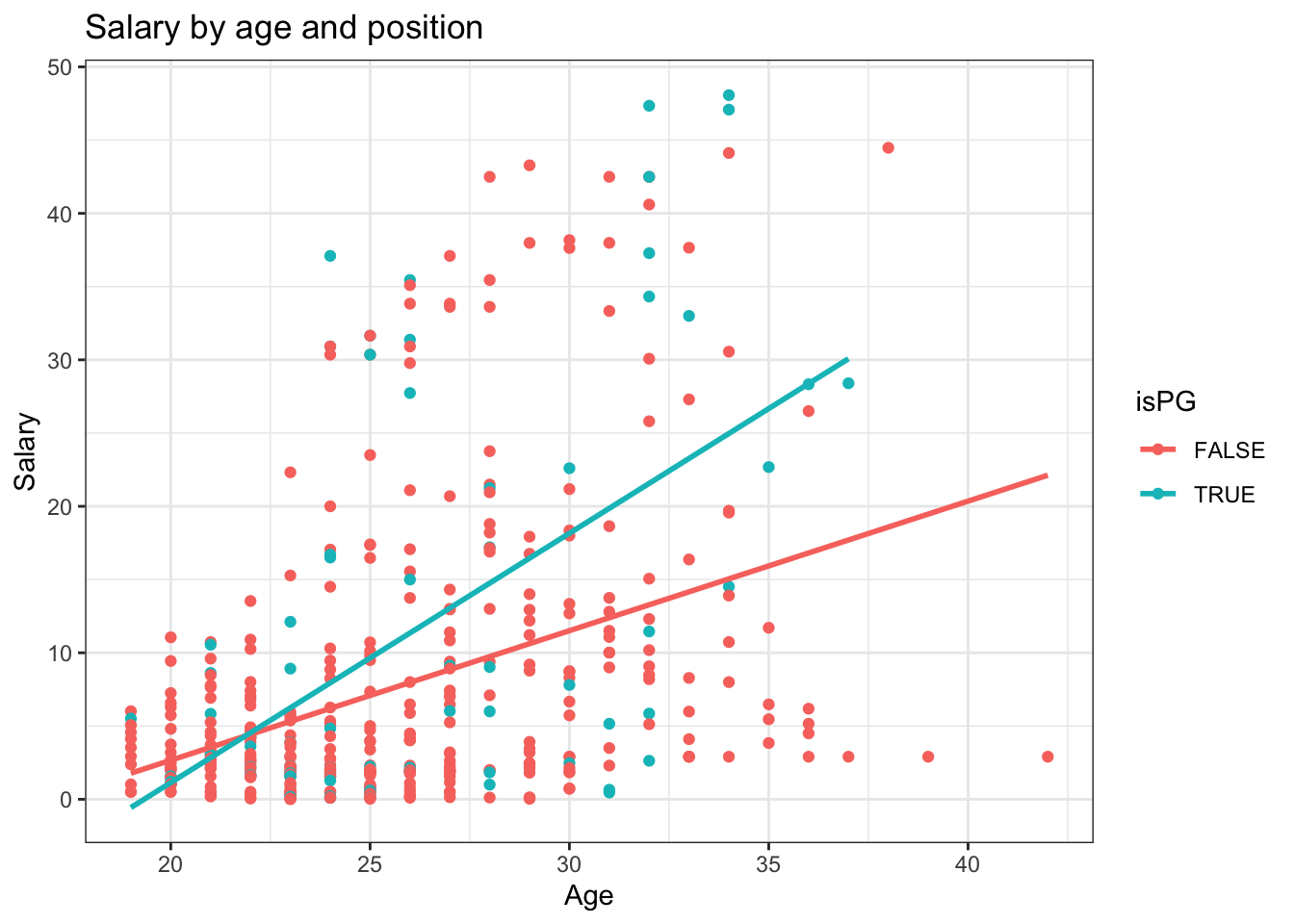
$ Salary <dbl> 48.07001, 47.34576, 47.08018, 44.47499, 44.11984, 43.279…
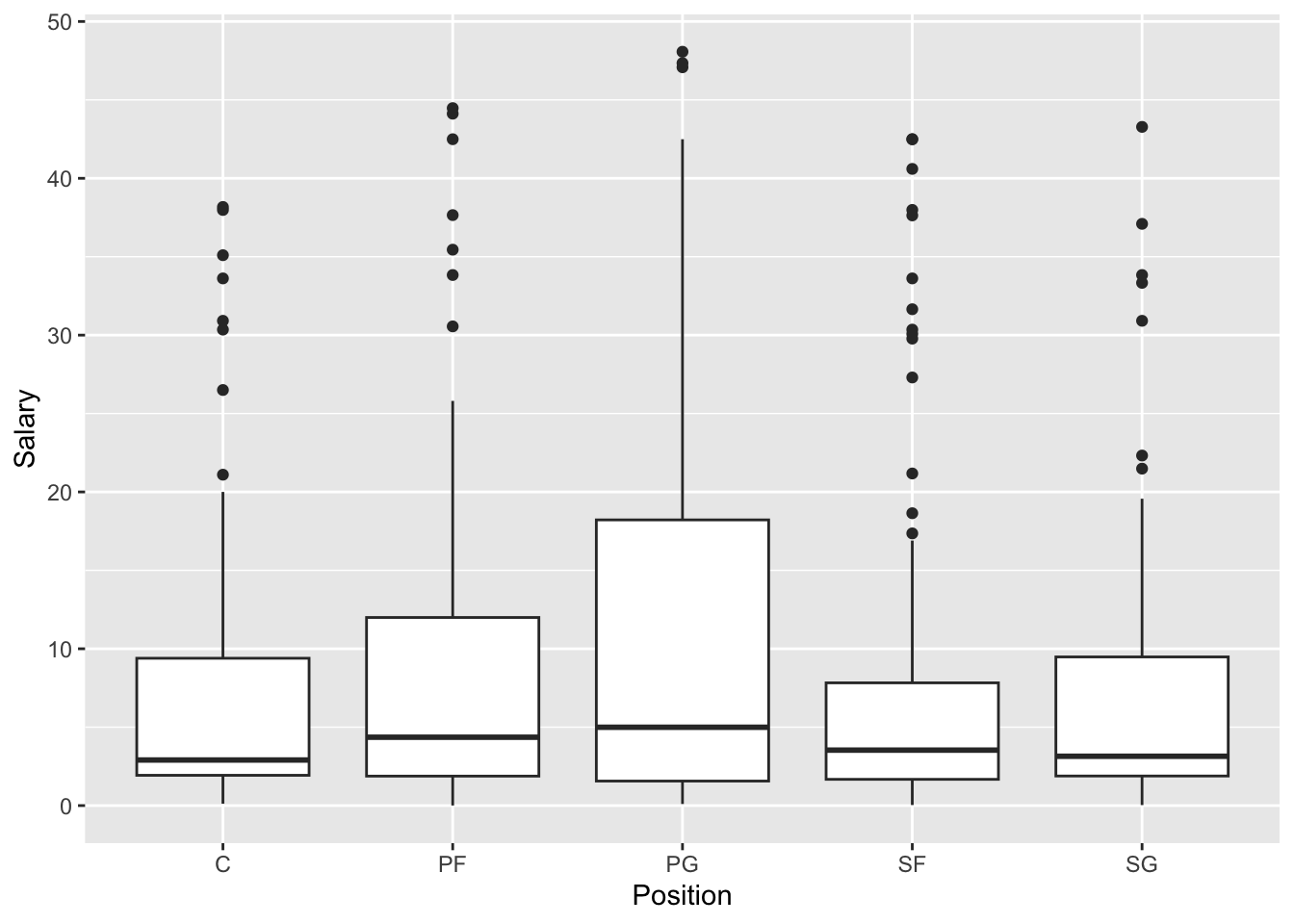
$ Position <chr> "PG", "PG", "PG", "PF", "PF", "SG", "SF", "SF", "PF", "P…
$ Age <dbl> 34, 32, 34, 38, 34, 29, 31, 32, 28, 32, 32, 30, 31, 29, …
$ GP <dbl> 56, 34, 73, 55, 47, 50, 52, 56, 63, 58, 69, 70, 33, 56, …
$ MP <dbl> 34.7, 22.2, 29.1, 35.5, 35.6, 33.5, 33.6, 34.6, 32.1, 36…
$ GS <dbl> 56, 3, 24, 54, 47, 50, 50, 56, 63, 58, 69, 70, 19, 54, 6…
$ FG <dbl> 10.0, 4.1, 5.9, 11.1, 10.3, 8.9, 8.6, 8.2, 11.2, 9.6, 7.…
$ `FG%` <dbl> 0.493, 0.408, 0.436, 0.500, 0.560, 0.506, 0.512, 0.457, …
$ `2PA` <dbl> 8.8, 6.7, 9.7, 15.3, 13.4, 13.2, 11.9, 10.3, 17.6, 9.4, …
$ `2P%` <dbl> 0.579, 0.459, 0.487, 0.580, 0.617, 0.552, 0.551, 0.521, …
$ AST <dbl> 6.3, 5.2, 7.5, 6.8, 5.0, 5.4, 3.9, 5.1, 5.7, 7.3, 2.4, 1…
$ `AST%` <dbl> 30.0, 35.3, 38.6, 33.5, 24.5, 26.6, 19.6, 24.2, 33.2, 35…