Multicollinearity

Author

Dr. Alexander Fisher

View libraries and data sets used in these notes 
# load packages
library(tidyverse)  
library(tidymodels)  
library(knitr)       
library(patchwork)
library(GGally)   # for pairwise plot matrix
library(corrplot) # for correlation matrix

# load data
rail_trail <- read_csv("https://sta221-fa25.github.io/data/rail_trail.csv")

# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Topics

  • Multicollinearity

    • Definition

    • How it impacts the model

    • How to detect it

    • What to do about it

Data: Trail users

  • The Pioneer Valley Planning Commission (PVPC) collected data at the beginning a trail in Florence, MA for ninety days from April 5, 2005 to November 15, 2005 to
  • Data collectors set up a laser sensor, with breaks in the laser beam recording when a rail-trail user passed the data collection station.

Source: Pioneer Valley Planning Commission via the mosaicData package.

Variables

Outcome:

  • volume estimated number of trail users that day (number of breaks recorded)

Predictors

  • hightemp daily high temperature (in degrees Fahrenheit)

  • avgtemp average of daily low and daily high temperature (in degrees Fahrenheit)

  • season one of “Fall”, “Spring”, or “Summer”

  • precip measure of precipitation (in inches)

EDA: Relationship between predictors

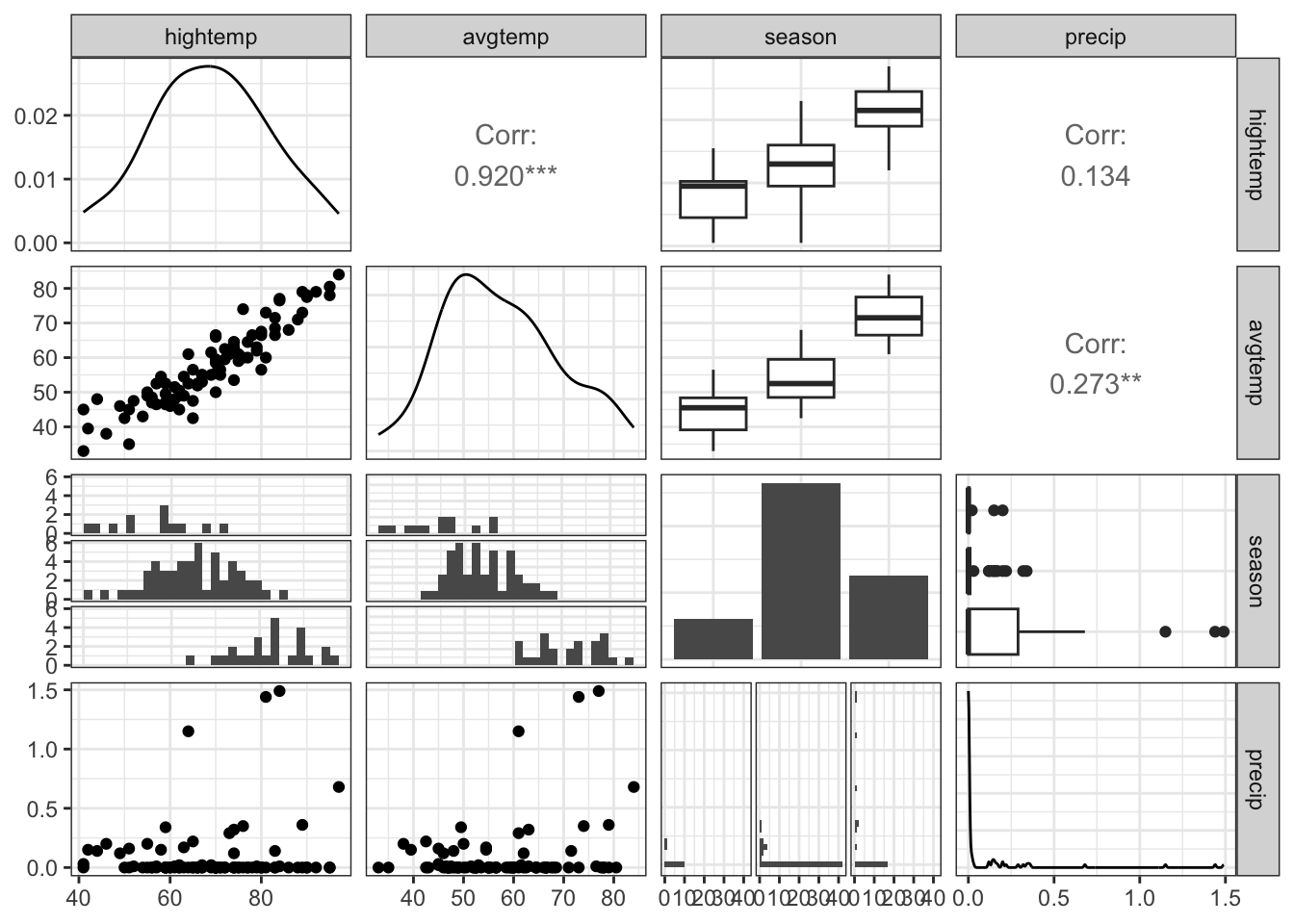
We can create a pairwise plot matrix using the ggpairs function from the GGally R package

rail_trail |>
  select(hightemp, avgtemp, season, precip) |>
  ggpairs()

EDA: Relationship between predictors

EDA: Correlation matrix

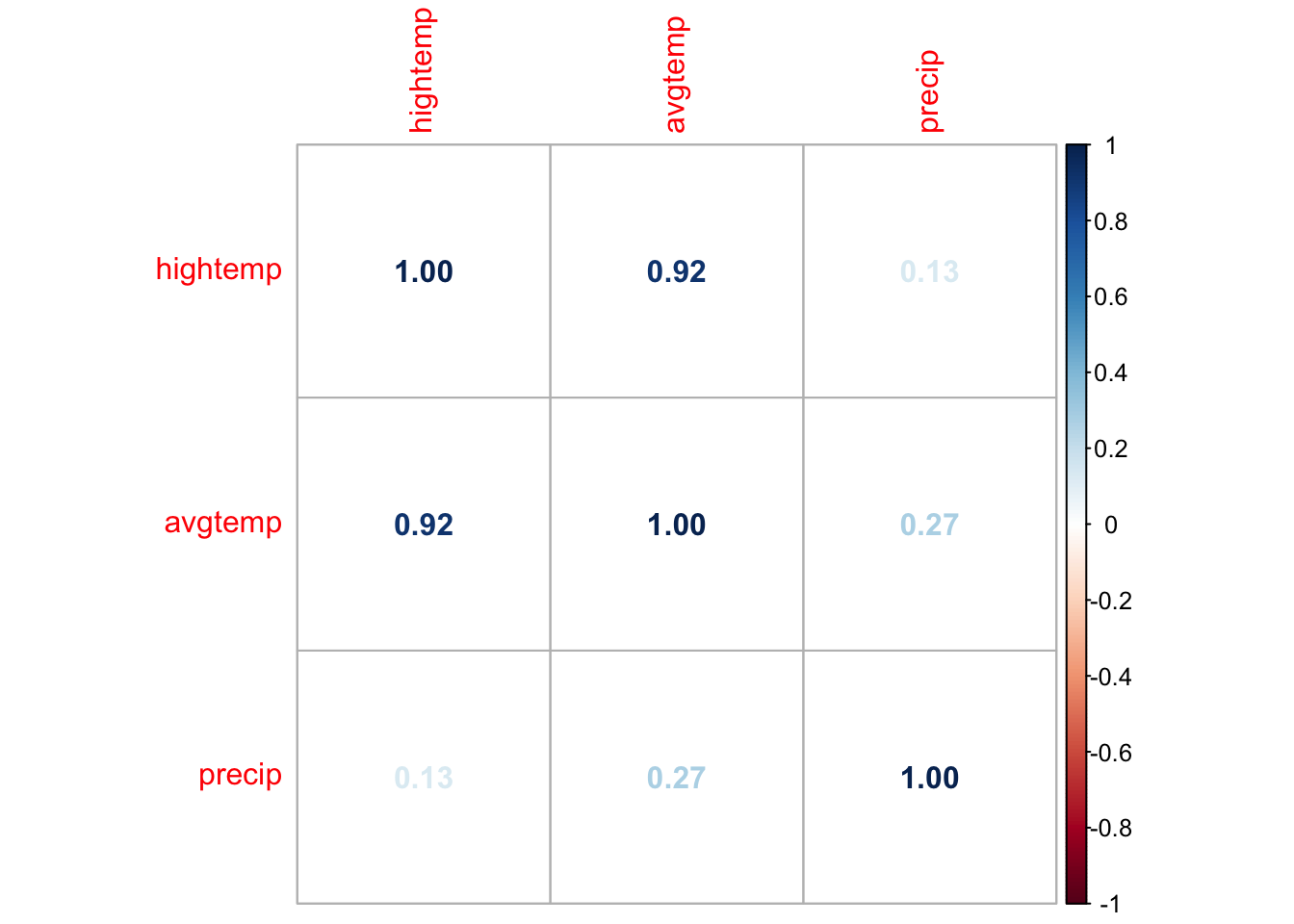
We can. use corrplot() in the corrplot R package to make a matrix of pairwise correlations between quantitative predictors

correlations <- rail_trail |>
  select(hightemp, avgtemp, precip) |>
  cor()

corrplot(correlations, method = "number")

EDA: Correlation matrix

What might be a potential concern with a model that uses high temperature, average temperature, season, and precipitation to predict volume?

Multicollinearity

Multicollinearity

  • Ideally the predictors are orthogonal, meaning they are completely independent of one another

  • In practice, there is typically some dependence between predictors but it is often not a major issue in the model

  • If there is linear dependence among (a subset of) the predictors, we cannot find estimate \(\hat{\boldsymbol{\beta}}\)

  • If there are near-linear dependencies, we can find \(\hat{\boldsymbol{\beta}}\) but there may be other issues with the model

  • Multicollinearity: near-linear dependence among predictors

Sources of multicollinearity

  • Data collection method - only sample from a subspace of the region of predictors

  • Constraints in the population - e.g., predictors family income and size of house

  • Choice of model - e.g., adding high order terms to the model

  • Overdefined model - have more predictors than observations

Detecting multicollinearity

How could you detect multicollinearity?

Variance inflation factor

  • The variance inflation factor (VIF) measures how much the linear dependencies impact the variance of the predictors

\[ VIF_{j} = \frac{1}{1 - R^2_j} \]

where \(R^2_j\) is the proportion of variation in \(x_j\) that is explained by a linear combination of all the other predictors

  • When the response and predictors are scaled in a particular way, \(C_{jj} = VIF_{j}\). Click here to see how.

Relationship with variance

Recall that \(Var(\hat{\beta}) = \sigma^2 (X^TX)^{-1}\). If we call the matrix \((X^TX)^{-1}\) “C” then the variance of \(\hat{\beta}_j\) is \(\sigma^2 C_{jj}\). Specifically,

\[ C_{jj} = VIF \times \frac{1}{\sum (X_{ij} - \bar{X_j})^2} \]

Detecting multicollinearity

  • Common practice uses threshold \(VIF > 10\) as indication of concerning multicollinearity (some say VIF > 5 is worth investigation)

  • Variables with similar values of VIF are typically the ones correlated with each other

  • Use the vif() function in the rms R package to calculate VIF

library(rms)

trail_fit <- lm(volume ~ hightemp + avgtemp + precip, data = rail_trail)

vif(trail_fit)
hightemp  avgtemp   precip 
7.161882 7.597154 1.193431

Load the data using the code below:

rail_trail <- read_csv("https://sta221-fa25.github.io/data/rail_trail.csv")

and compute VIF manually (without using the function vif()).

How multicollinearity impacts model

  • Large variance for the model coefficients that are collinear

    • Different combinations of coefficient estimates produce equally good model fits

  • Unreliable statistical inference results

    • May conclude coefficients are not statistically significant when there is, in fact, a relationship between the predictors and response

  • Interpretation of coefficient is no longer “holding all other variables constant”, since this would be impossible for correlated predictors

Dealing with multicollinearity

  • Collect more data (often not feasible given practical constraints)

  • Redefine the correlated predictors to keep the information from predictors but eliminate collinearity

    • e.g., if \(x_1, x_2, x_3\) are correlated, use a new variable \((x_1 + x_2) / x_3\) in the model

  • For categorical predictors, avoid using levels with very few observations as the baseline

  • Remove one of the correlated variables

    • Be careful about substantially reducing predictive power of the model

Recap

  • Introduced multicollinearity

    • Definition

    • How it impacts the model

    • How to detect it

    • What to do about it

End of class notes

library(tidyverse)
library(tidymodels)

rail_trail <- read_csv("https://sta221-fa25.github.io/data/rail_trail.csv")

model1 <- lm(hightemp ~ avgtemp + precip, data = rail_trail)
1 / (1 - glance(model1)$r.squared)

set.seed(221)
rt_split = initial_split(rail_trail, prop = 3/4)
rt_train = training(rt_split)
rt_test = testing(rt_split)

model_full <- lm(volume ~ hightemp + avgtemp + precip, data = rt_train)
model_minus_temp <- lm(volume ~ avgtemp + precip, data = rt_train)

residual_full <- rt_test$volume - predict(model_full, newdata = rt_test)
residual_minus_temp <- rt_test$volume -
  predict(model_minus_temp, newdata = rt_test)

## Compare root mean squared error (RMSE)
sqrt(sum(residual_full^2))
sqrt(sum(residual_minus_temp^2))

## Examine coefficients for each model
model_full
model_minus_temp