Multiple linear regression

Author

Dr. Alexander Fisher

View libraries and data sets used in these notes 
library(tidyverse)
library(palmerpenguins)
library(tidymodels)
library(scatterplot3d)
library(DT)

Illustration of a linear model

Example

Imagine we’ve collected 3 measurements on a number of penguins:

  • body mass (g)
  • bill length (mm)
  • flipper length (mm)
Data

Read more about the data here.

The first five entries of our data set are given below:

# A tibble: 5 × 3
  body_mass_g bill_length_mm flipper_length_mm
        <int>          <dbl>             <int>
1        3750           39.1               181
2        3800           39.5               186
3        3250           40.3               195
4        3450           36.7               193
5        3650           39.3               190

In all, our data set contains the measurements of 342 penguins. Because we’ve collected three measurements, each individual penguin can be represented as a point in three dimensional space:

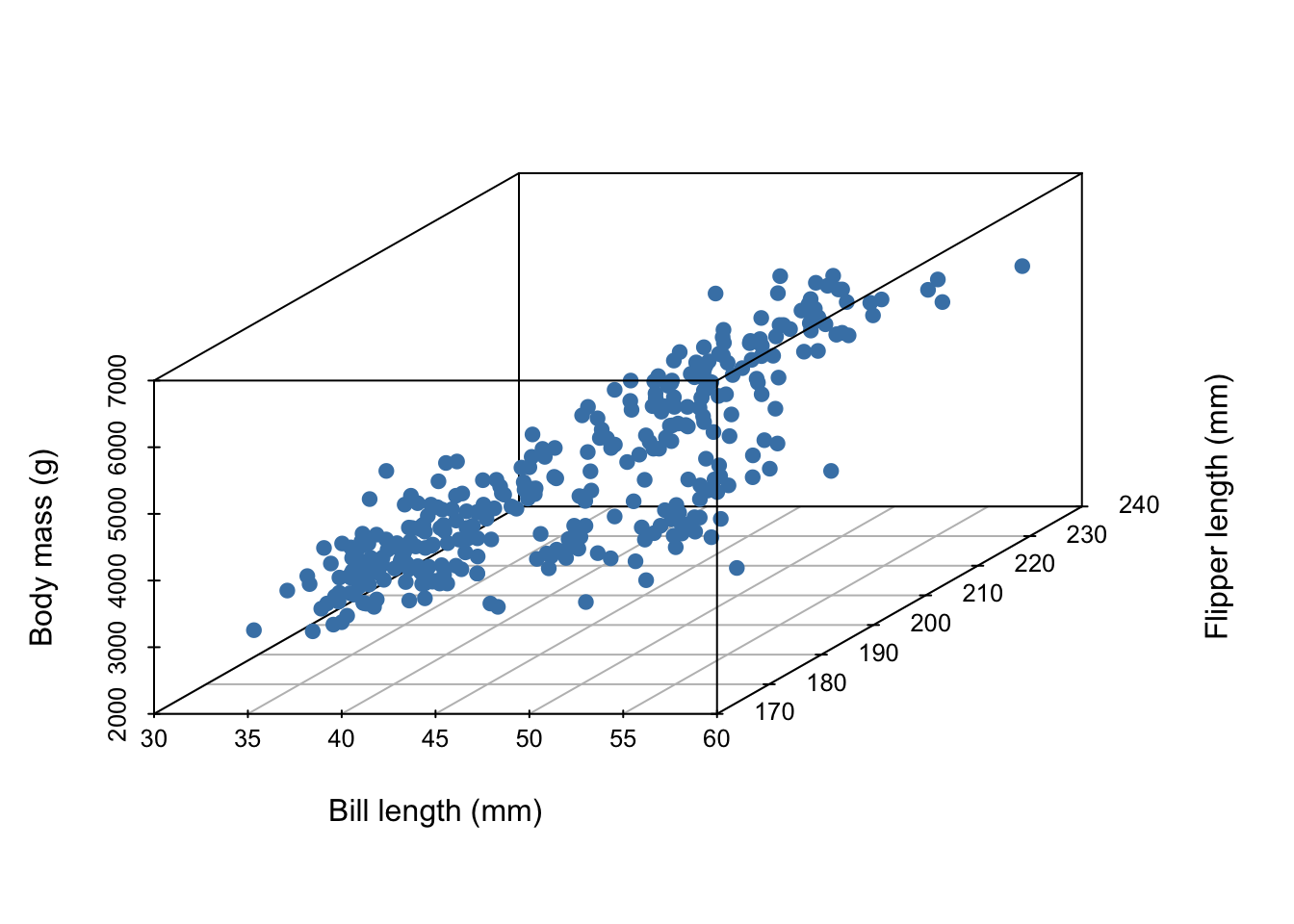
Now, imagine it’s hard to measure a penguin’s bodymass because it’s difficult to get them onto a scale. We wish to develop a linear model that uses bill length and flipper length to predict body mass,

\[ E[Y|X] = X \beta, \]

where

  • \(Y\) is the body mass of the penguins and
  • \(X\) contains covariates bill length and flipper length.

What does our linear model look like?

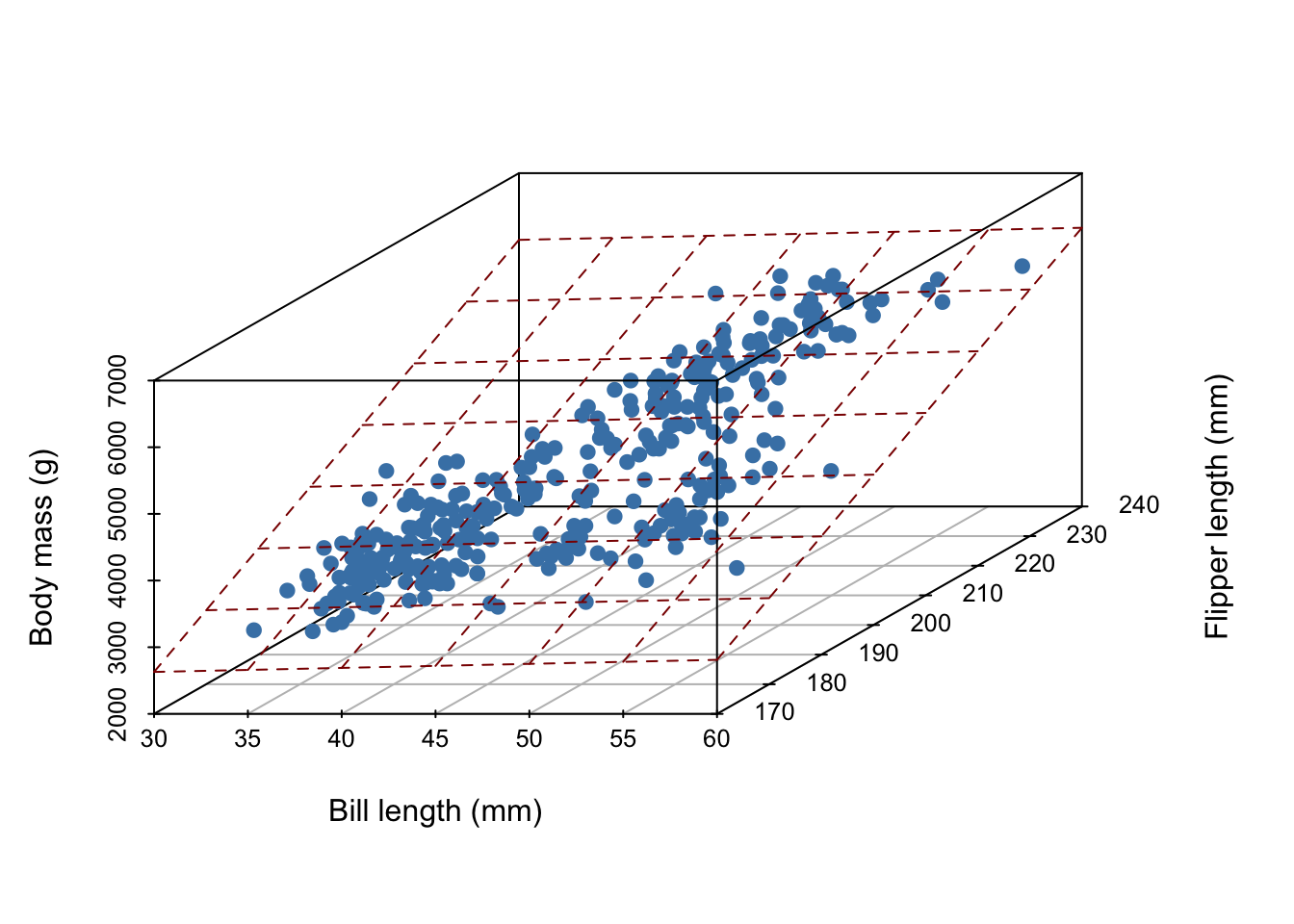
In general, for \(D\) measurements, a linear model is a \(D-1\) dimensional hyperplane!

Fitting a regression model

To “fit” a (multiple) linear regression model means finding \(\hat{\beta}\) that defines the “best” hyperplane. Here, “best” means that \(\hat{\beta}\) is the optimal solution of some objective function.

Full data set

datatable(penguins, rownames = FALSE, options = list(pageLength = 5),
           caption = "penguins")

Write down the mathematical formula for linear regression where penguin bodymass is the outcome variable and flipper length, bill length, and sex of the penguin are the covariates. Note the dimension of each symbol in your model.

\[ \boldsymbol{y}= \boldsymbol{X}\beta + \boldsymbol{\varepsilon} \]

As usual,

  • \(\boldsymbol{y}, \boldsymbol{\varepsilon}\in \mathbb{R}^n\)
  • \(\boldsymbol{X}\in \mathbb{R}^{n \times p}\)
  • \(\beta \in \mathbb{R}^p\)

but here \(p = 4\) (3 covariates + intercept).

\[ \boldsymbol{X}= \begin{bmatrix} \vdots & \vdots & \vdots & \vdots \\ \mathbf{1} & \mathbf{x}_1 & \mathbf{x}_2 & \mathbf{x}_3 \\ \vdots & \vdots & \vdots & \vdots \end{bmatrix} \]

Question: Why is sex (a categorical predictor) represented as 1 column and not 2?

Answer: It would create a linearly dependent column in the matrix \(\boldsymbol{X}\), then \(\boldsymbol{X}^T \boldsymbol{X}\) would be rank deficient and could not be inverted.

Question: Suppose we add the covariate “island”, what is the new dimension of \(\boldsymbol{X}\) and \(\beta\) then?

Answer: Island is categorical with three states, therefore we would need 2 predictors to represent it. Now \(p = 6\) and \(\boldsymbol{X}\in \mathbb{R}^{n \times 6}\) and \(\beta \in \mathbb{R}^6\).

Fitting multiple regression in R (OLS)

The formula for the least squares estimator \(\hat{\beta}_{OLS}\) is the same,

\[ \hat{\beta}_{OLS} = \left(\boldsymbol{X}^T \boldsymbol{X}\right)^{-1} \boldsymbol{X}^T \boldsymbol{y} \]

penguin_fit <- lm(body_mass_g ~ flipper_length_mm + bill_length_mm +  sex + island, data = penguins)

penguin_fit

Call:
lm(formula = body_mass_g ~ flipper_length_mm + bill_length_mm + 
    sex + island, data = penguins)

Coefficients:
      (Intercept)  flipper_length_mm     bill_length_mm            sexmale  
        -3629.563             37.638              5.808            390.055  
      islandDream    islandTorgersen  
         -376.124           -288.380

Question: Why didn’t I have to specify an intercept?

Answer: lm includes intercept by default.

Question: What if I don’t want an intercept?

Answer: Use + 0, like this: lm(y ~ x1 + x2 + ... + x_5 + 0, data = penguin). This will tell lm not to exclude an intercept term from the model.

yX <- penguins %>%
  select(c("body_mass_g", "bill_length_mm", "flipper_length_mm",
           "sex", "island")) %>%
  mutate(isMale = ifelse(sex == "male", 1, 0), ## create 1 dummy variable 
           isDream = ifelse(island == "Dream", 1, 0), ## create other 2 dummy variables
         isTorgersen = ifelse(island == "Torgersen", 1, 0)) %>%
  select(-c(island, sex)) %>% ## remove redundant columns 
  mutate(one = 1) %>% # create vector of ones
  drop_na() %>% # drop NAs, just like the lm() function does by default
  as.matrix() # turn into a matrix for matrix algebra in R

y <- yX[,1] # grab first column (which was the outcome variable)
X <- yX[,-1] # grab all but first column (X matrix)

betaHat <- solve(t(X) %*% X) %*% t(X) %*% y
betaHat
                          [,1]
bill_length_mm        5.808086
flipper_length_mm    37.637788
isMale              390.055414
isDream            -376.124225
isTorgersen        -288.380366
one               -3629.562552

An alternative, easy way to grab \(X\) quickly:

X = model.matrix( body_mass_g ~ flipper_length_mm + bill_length_mm +  sex + island,
              data = penguins)
X %>%
  head(n = 10) # notice NAs are dropped by default, (see the row number skips)
   (Intercept) flipper_length_mm bill_length_mm sexmale islandDream
1            1               181           39.1       1           0
2            1               186           39.5       0           0
3            1               195           40.3       0           0
5            1               193           36.7       0           0
6            1               190           39.3       1           0
7            1               181           38.9       0           0
8            1               195           39.2       1           0
13           1               182           41.1       0           0
14           1               191           38.6       1           0
15           1               198           34.6       1           0
   islandTorgersen
1                1
2                1
3                1
5                1
6                1
7                1
8                1
13               1
14               1
15               1

Interpretation

Slopes

We interpret slopes \(\hat{\beta}_j\) as the expected change in the mean of \(Y\) when \(X_j\) increases by one unit, holding the value of all other predictor variables constant.

For example, for each additional mm of flipper length a given penguin has, we expect their body mass to increase by 37.6 grams holding all other covariates constant.

Intercept

The intercept is the expected value of \(Y\) when all predictors are zero. Note: when there is a categorical predictor, this corresponds to some “default” category.

Prediction

We can still make predictions in R; now we require more covariates. For example:

new_penguin <- tibble(
  flipper_length_mm = 180, 
  bill_length_mm = 40,
  sex = "male",
  island = "Dream"
)

cat("The predicted body mass of the new penguin is:\n")
The predicted body mass of the new penguin is:
predict(penguin_fit, new_penguin)
       1 
3391.494
Warning

Regression shows association not causality.